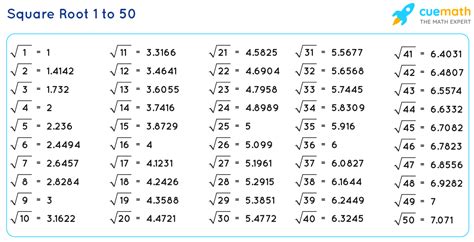
The square root of 50 is a mathematical operation that involves finding a number that, when multiplied by itself, gives the result of 50. To calculate this, we use the mathematical symbol √, which denotes the square root operation. In the case of √50, we are looking for a number x such that x * x = 50.
Natural Calculation Approach
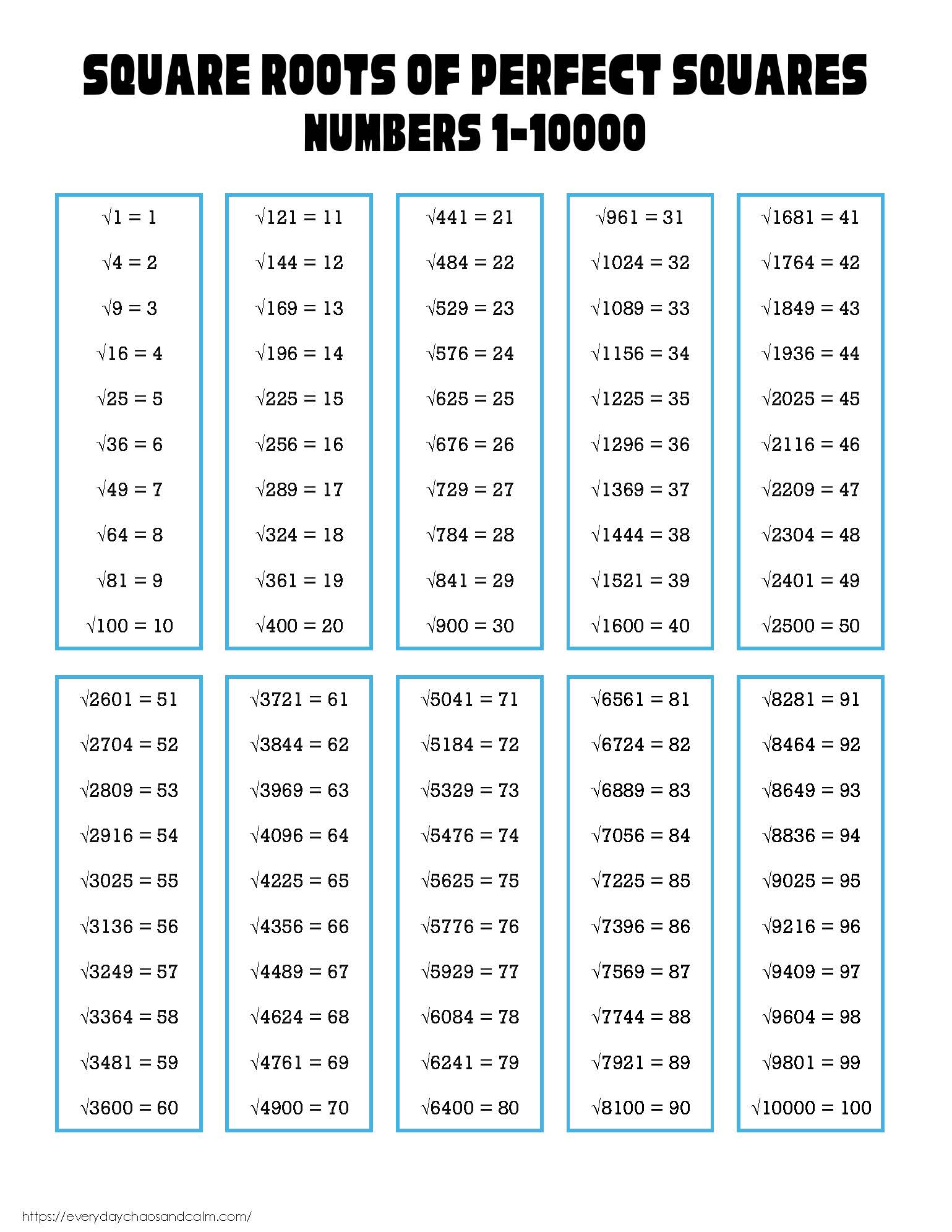
A straightforward approach to finding the square root of 50 involves factoring 50 into prime factors to see if it simplifies the calculation. 50 can be factored into 2 * 5 * 5. Since we have a pair of 5s, we can simplify √50 to 5√2, because the pair of 5s can be taken out of the square root as a single 5, leaving one 2 inside the square root.
Approximation and Calculation
For a more precise numerical value, we calculate the square root of 2, as that is the only part not simplified in our expression 5√2. The square root of 2 is approximately 1.414. Therefore, multiplying this by 5 gives us an approximate value for the square root of 50: 5 * 1.414 = 7.07. This is a more precise numerical answer to the question of what the square root of 50 is.
| Mathematical Operation | Value |
|---|---|
| √50 | 5√2 |
| Approximation of √2 | 1.414 |
| Approximate Value of √50 | 7.07 |

Key Points
- The square root of 50 can be simplified to 5√2 by factoring 50 into prime factors.
- The approximate numerical value of the square root of 50 is 7.07, found by multiplying 5 by the approximate value of √2, which is 1.414.
- Both positive and negative square roots exist; hence, the square roots of 50 are approximately 7.07 and -7.07.
- Understanding the square root operation involves recognizing that it seeks a number that, when squared, gives the original number.
- Approximations are useful for practical applications but may lack the precision required in certain mathematical or scientific contexts.
Mathematical Context and Applications

The calculation of square roots is fundamental in mathematics and has numerous applications in physics, engineering, and other fields. For instance, in geometry, finding the length of a side of a square given its area involves calculating the square root of the area. Similarly, in physics, certain formulas, such as those related to the frequency of a pendulum or the period of a wave, involve square root operations.
Practical Considerations
In practical applications, the ability to quickly estimate or calculate square roots can be beneficial. For example, in construction or design, knowing the square root of a number can help in determining dimensions or proportions of shapes and structures. Furthermore, understanding how to simplify and approximate square roots, as demonstrated with the calculation of √50, enhances problem-solving skills in a variety of mathematical and real-world contexts.
As we consider the square root of 50 and its applications, it's clear that mathematical operations like these underpin many aspects of our understanding of the world, from the simplest geometric calculations to complex scientific formulas. The ability to calculate, approximate, and apply such operations is crucial for advancing in fields that rely heavily on mathematical precision and conceptual understanding.
What is the square root of 50 in simplified form?
+The square root of 50 can be simplified to 5√2 by factoring 50 into its prime factors, which are 2 * 5 * 5.
How do you approximate the square root of 50?
+To approximate the square root of 50, you first simplify it to 5√2. Then, using the approximation of √2 as 1.414, you multiply this by 5 to get an approximate value of 7.07.
What are the positive and negative square roots of 50?
+The positive square root of 50 is approximately 7.07, and the negative square root of 50 is approximately -7.07, based on the calculation and approximation of 5√2.