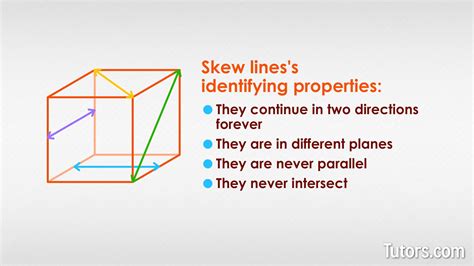
Skew lines are a fundamental concept in geometry, particularly in three-dimensional space. They refer to two lines that do not intersect each other and are not parallel. This means that skew lines are not contained in the same plane and do not have any points in common. To understand skew lines, it's essential to differentiate them from parallel lines, which never intersect but lie in the same plane, and intersecting lines, which cross each other at a single point.
Key Points
- Skew lines are lines that do not intersect and are not parallel.
- They do not lie in the same plane.
- Skew lines have no points in common.
- Understanding skew lines requires a grasp of three-dimensional geometry.
- Skew lines are distinct from parallel and intersecting lines.
Characteristics of Skew Lines

Skew lines have several key characteristics that distinguish them from other types of lines in geometry. Firstly, they are non-coplanar, meaning they do not exist in the same plane. This is what sets them apart from parallel lines, which may never intersect but are always found within the same plane. Secondly, skew lines do not share any common points; they never touch or cross each other. This characteristic is crucial for understanding the spatial relationships between lines in three-dimensional geometry.
Visualizing Skew Lines
Visualizing skew lines can be challenging because it requires thinking about three-dimensional space. A common way to illustrate skew lines is by considering two lines that pass through different parts of a cube without intersecting. For instance, one line might run from the top left corner of the cube to the bottom right corner, while the other line goes from the top right corner to the bottom left corner. These lines do not intersect because they are not in the same plane, and they are not parallel because they are not contained within the same plane.
| Property | Description |
|---|---|
| Non-coplanar | Skew lines do not exist in the same plane. |
| No Common Points | Skew lines never touch or intersect. |
| Three-dimensional | Skew lines are a concept of 3D geometry. |

Applications of Skew Lines

Skew lines have practical applications in various fields. In architecture, understanding how lines and shapes interact in three-dimensional space is crucial for designing structures. Engineers also rely on the concept of skew lines when designing mechanisms and systems that operate in three-dimensional environments. Furthermore, computer graphics and animation heavily utilize the principles of 3D geometry, including the concept of skew lines, to create realistic and engaging visual effects.
Mathematical Representation
The mathematical representation of skew lines involves vectors and direction numbers. Two lines are skew if their direction vectors are not parallel and if there is no vector that connects a point on one line to a point on the other line. Mathematically, if we have two lines defined by their parametric equations, we can determine if they are skew by checking if their direction vectors are not proportional (indicating they are not parallel) and if the system of equations formed by equating the parametric equations of the two lines has no solution (indicating they do not intersect).
What is the main characteristic of skew lines?
+The main characteristic of skew lines is that they do not intersect and are not parallel, meaning they do not lie in the same plane.
How do skew lines differ from parallel lines?
+Skew lines differ from parallel lines in that they do not exist in the same plane, whereas parallel lines do.
What are some practical applications of skew lines?
+Skew lines have applications in architecture, engineering, and computer graphics, where understanding spatial relationships in three-dimensional space is crucial.
In conclusion, skew lines are a fundamental concept in geometry that highlights the complexities of spatial relationships in three-dimensional space. Their characteristics, applications, and mathematical representations underscore their importance in both theoretical geometry and practical fields. As we delve deeper into the intricacies of geometry, understanding skew lines provides a deeper appreciation for the intricacies of spatial relationships and their role in shaping our understanding of the world around us.