The concept of tangential acceleration is a fundamental aspect of physics and engineering, particularly in the study of rotational motion. It is a measure of how the speed of an object changes as it moves along a circular path. The tangential acceleration formula is a crucial tool for calculating this type of acceleration, and it has numerous applications in fields such as mechanics, robotics, and aerospace engineering. In this article, we will delve into the world of tangential acceleration, exploring its definition, the formula used to calculate it, and its significance in various real-world scenarios.
Understanding Tangential Acceleration
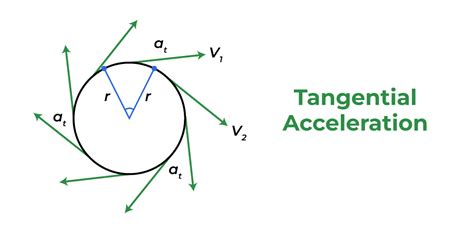
Tangential acceleration is a vector quantity that describes the rate of change of an object’s speed as it moves along a circular trajectory. It is directed tangent to the circle at the point of interest and is typically denoted by the symbol “a_t”. The tangential acceleration formula is given by the equation: a_t = dv/dt, where “dv” represents the change in speed and “dt” is the time over which this change occurs. This formula is a direct application of the definition of acceleration, which is the rate of change of velocity.
Tangential Acceleration Formula Derivation
The derivation of the tangential acceleration formula involves the use of calculus and the concept of limits. Starting with the definition of acceleration as the derivative of velocity with respect to time, we can express the tangential acceleration as the derivative of the tangential velocity component. This results in the equation: a_t = d(v * cos(θ))/dt, where “v” is the magnitude of the velocity vector and “θ” is the angle between the velocity vector and the tangent to the circle. Simplifying this expression, we arrive at the formula: a_t = dv/dt, which is the fundamental equation for calculating tangential acceleration.
| Quantity | Symbol | Unit |
|---|---|---|
| Tangential Acceleration | a_t | m/s^2 |
| Change in Speed | dv | m/s |
| Time | dt | s |

Applications of Tangential Acceleration
Tangential acceleration has numerous practical applications in various fields, including mechanics, robotics, and aerospace engineering. For instance, in the design of circular motion systems, such as centrifuges or spinning tops, understanding tangential acceleration is crucial for predicting the motion of objects and ensuring safe operation. Additionally, in the field of robotics, tangential acceleration is used to control the motion of robotic arms and grippers, allowing for precise manipulation of objects.
Example Calculations
To illustrate the use of the tangential acceleration formula, consider a car moving along a circular track with a radius of 50 meters. If the car’s speed increases from 10 m/s to 20 m/s in a time period of 5 seconds, we can calculate its tangential acceleration as follows: a_t = (20 m/s - 10 m/s) / 5 s = 2 m/s^2. This result indicates that the car is accelerating tangentially at a rate of 2 meters per second squared.
Key Points
- The tangential acceleration formula is given by the equation: a_t = dv/dt
- Tangential acceleration is a vector quantity that describes the rate of change of an object's speed as it moves along a circular trajectory
- The formula has numerous applications in fields such as mechanics, robotics, and aerospace engineering
- Understanding tangential acceleration is crucial for predicting the motion of objects and ensuring safe operation in circular motion systems
- The formula can be used to calculate the tangential acceleration of objects in various real-world scenarios
Conclusion and Future Directions
In conclusion, the tangential acceleration formula is a fundamental concept in physics and engineering, with numerous applications in various fields. By understanding and applying this formula, engineers and scientists can analyze and predict the motion of objects in circular trajectories, leading to improvements in design, safety, and efficiency. As technology continues to advance, the importance of tangential acceleration will only continue to grow, driving innovation and discovery in fields such as robotics, aerospace engineering, and beyond.
What is the difference between tangential and centripetal acceleration?
+Tangential acceleration is the rate of change of an object’s speed as it moves along a circular trajectory, while centripetal acceleration is the rate of change of an object’s direction. Both types of acceleration are essential for understanding the motion of objects in circular paths.
How is the tangential acceleration formula used in real-world applications?
+The tangential acceleration formula is used in various fields, including mechanics, robotics, and aerospace engineering, to analyze and predict the motion of objects in circular trajectories. It is essential for designing safe and efficient systems, such as centrifuges, spinning tops, and robotic arms.
What are the limitations of the tangential acceleration formula?
+The tangential acceleration formula only accounts for changes in speed and not changes in direction. For a complete understanding of an object’s motion, it is necessary to consider both tangential and normal (or centripetal) acceleration components.
