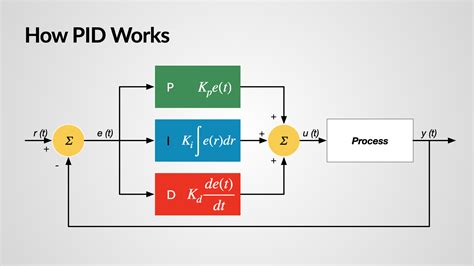
The term "PID loop" refers to a control loop mechanism widely used in industrial control systems to regulate and maintain a desired setpoint for a specific process variable. PID stands for Proportional, Integral, and Derivative, which are the three primary components that make up the control algorithm. Understanding the PID loop meaning requires delving into the roles of these components and how they interact to achieve precise control over processes such as temperature, pressure, flow rate, and more.
Components of a PID Loop

A PID loop consists of a controller, a sensor or measurement device, and an actuator or control element. The sensor monitors the process variable and provides feedback to the controller, which then adjusts the actuator to achieve the desired setpoint. The PID algorithm within the controller calculates the difference between the setpoint and the actual process variable, known as the error, and applies corrections based on the proportional, integral, and derivative terms.
Proportional (P) Term
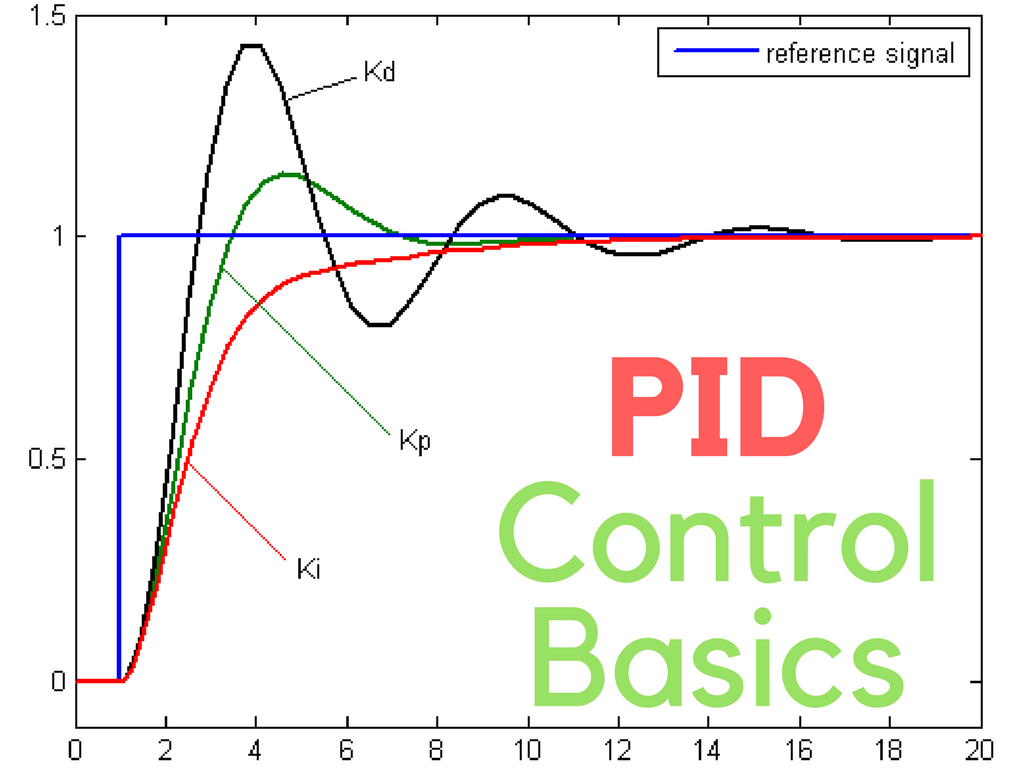
The proportional term is directly related to the current error value. It adjusts the output of the controller by a factor proportional to the error. A high proportional gain means that the controller will make large adjustments for small errors, which can lead to oscillations around the setpoint. The proportional term provides an immediate response to changes in the process variable but may not be sufficient on its own to eliminate steady-state error.
Integral (I) Term
The integral term adjusts the controller output based on the accumulation of past errors over time. It aims to eliminate the steady-state error by increasing or decreasing the output if the error persists. The integral term has a significant effect when the process variable is not at the setpoint, and its action continues until the error is zero. However, if the integral gain is too high, it can cause the system to overshoot and oscillate.
Derivative (D) Term
The derivative term is based on the rate of change of the error over time. It predicts future errors and makes adjustments to prevent them, thus acting as a damping factor on the system. The derivative term is particularly useful in systems with a lot of inertia, where changes to the process variable are slow, and anticipating these changes can help in achieving the setpoint more efficiently. However, if the derivative gain is too high, it can amplify noise in the system, leading to undesirable oscillations.
Tuning a PID Loop
Tuning a PID loop involves adjusting the proportional, integral, and derivative gains to achieve optimal performance in terms of stability, responsiveness, and accuracy. There are several methods for tuning PID loops, including the Ziegler-Nichols method, which provides a systematic approach to determining the gains. Tuning is critical because the performance of the PID loop can significantly affect the efficiency, safety, and product quality of the process being controlled.
| PID Term | Description | Effect |
|---|---|---|
| Proportional (P) | Adjusts output based on current error | Immediate response, potential for oscillation |
| Integral (I) | Adjusts output based on accumulation of past errors | Eliminates steady-state error, risk of overshoot |
| Derivative (D) | Adjusts output based on rate of change of error | Predicts and prevents future errors, sensitive to noise |
Key Points
- A PID loop is a control mechanism used to regulate process variables by adjusting the proportional, integral, and derivative terms.
- The proportional term provides an immediate response to errors, the integral term eliminates steady-state errors, and the derivative term predicts and prevents future errors.
- Tuning the PID loop involves adjusting the gains of the P, I, and D terms to achieve optimal performance, considering factors such as stability, responsiveness, and accuracy.
- The Ziegler-Nichols method is a systematic approach to tuning PID loops, providing a starting point for further adjustments based on the specific process characteristics.
- The balance between the P, I, and D terms is critical for achieving stable and efficient control, with improper tuning leading to issues such as oscillations, overshooting, and steady-state errors.
Applications and Limitations of PID Loops
PID loops are widely used in various industries, including process control, robotics, and automotive systems, due to their simplicity and effectiveness in controlling a broad range of processes. However, they also have limitations, such as sensitivity to noise and the potential for oscillations if not properly tuned. In complex systems or those with non-linear dynamics, more advanced control strategies, such as model predictive control or adaptive control, may be necessary.
In conclusion, understanding the PID loop meaning and its components is essential for designing and implementing effective control systems. By carefully tuning the proportional, integral, and derivative gains, engineers can achieve precise control over process variables, enhancing efficiency, safety, and product quality in a wide range of applications.
What is the primary purpose of a PID loop in control systems?
+The primary purpose of a PID loop is to maintain a process variable at a desired setpoint by adjusting the control output based on the proportional, integral, and derivative terms.
How do you tune a PID loop for optimal performance?
+Tuning a PID loop involves adjusting the gains of the P, I, and D terms. Methods like the Ziegler-Nichols method provide a systematic approach to determining these gains, which can then be fine-tuned based on the specific process characteristics and performance requirements.
What are the limitations of PID loops in control systems?
+PID loops can be sensitive to noise and may not perform well in systems with complex or non-linear dynamics. In such cases, more advanced control strategies may be necessary to achieve optimal performance.