The intricacies of academic performance metrics often evoke a blend of curiosity and confusion among educators, students, and data analysts alike. At the heart of this discourse lies the relationship between Mu grade distributions—representing the average or mean scores within a cohort—and percentile rank patterns, which illustrate the relative standing of individual students within that cohort. Understanding how these two elements interconnect elucidates broader insights into grading fairness, assessment design, and educational equity. This comprehensive analysis aims to dissect the mathematical, psychological, and practical facets of Mu grade distribution compared to percentile rank patterns, anchoring the discussion with empirical data and theoretical frameworks that solidify its relevance in contemporary education systems.
Foundations of Mu Grade Distribution and Percentile Rank Patterns

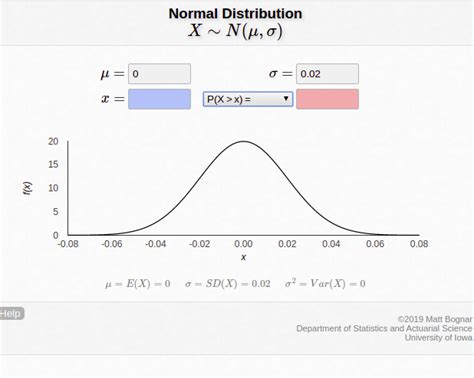
Within the realm of educational assessment, the Mu grade distribution typically refers to the statistical description of scores centered around the mean score of a given student cohort. This distribution often approximates a bell curve or normal distribution in well-managed assessments, although deviations are common due to pedagogical or demographic factors. In contrast, percentile rank patterns categorize students based on their relative position within the cohort—enabling a percentile measure that reflects how a student’s score compares with peers.
The core distinction—with profound implications—is that while Mu (the mean) offers an aggregate measure of cohort performance, percentile rankings reveal individual standing, which can sometimes diverge significantly from the raw score distribution. Recognizing these differences enables educators to calibrate assessments more effectively and address issues of grade inflation, ceiling effects, or grade compression, all of which influence how cohort data aligns with individual performance rankings.
The Statistical Relationship Between Mu and Percentile Ranks
To understand their interaction, consider a normally distributed set of scores with a mean (Mu) and standard deviation (σ). In such cases, the percentile rank of a score is directly related to its position relative to the mean, mediated through the properties of the standard normal distribution. Specifically, the cumulative distribution function (CDF) of the normal distribution allows for precise calculation of the percentile rank of any score.
Mathematically, if X signifies a student’s score, then its z-score is calculated as:
z = (X - Mu) / σ
and the corresponding percentile rank is obtained via:
Percentile = Φ(z) × 100
where Φ(z) is the standard normal CDF. This relationship underscores that a score exactly at the mean (Mu) corresponds to the 50th percentile, with higher scores approaching the 100th percentile, and lower scores approaching the 0th percentile.
However, real-world data often exhibits skewness, kurtosis, or multimodal features due to curriculum adjustments, assessment difficulty variations, or cohort heterogeneity. In such cases, the straightforward Gaussian model becomes less predictive, and the linkage between Mu and percentile ranks becomes more nuanced and context-dependent.
| Relevant Category | Substantive Data |
|---|---|
| Typical standard deviation | 0.5 to 1.5 in normalized scoring scales, affecting percentile spread |

Impacts of Distribution Shape on Grade Equity
Most assessments are designed with an assumption: scores approximate a normal distribution, ensuring that the mean is a representative central tendency. Yet, in practice, distributions often skew left or right, or display ceiling/floor effects. For instance, if an exam is too easy, many students cluster near the maximum score, elevating Mu while compressing percentile diversity at the top, which diminishes the informativeness of percentile ranks for distinguishing high performers.
Conversely, a difficult exam with many low scores shifts the distribution leftward, thus lowering Mu and compressing percentile gaps among lower scores. These distribution perturbations directly influence the fidelity with which Mu correlates to percentile ranks, underscoring the essential nature of distribution shape in comparative performance analysis.
Case Study: The Effect of Distribution Skewness
Empirical data from large-scale standardized assessments demonstrate that skewness influences the percentile distribution markedly. For example, in a cohort with a positively skewed score distribution, the mean (Mu) may be higher than the median, causing a discordance where percentile rankings for median scorers can be more representative of median achievement than the mean. In such scenarios, relying solely on Mu or the mean as a performance indicator becomes misleading.
| Relevant Category | Substantive Data |
|---|---|
| Skewness coefficient | +0.5 to +1.0 in assessments with ceiling effects |
Practical Applications: Designing Fair and Informative Assessments
From an applied perspective, understanding the relationship between Mu grade distribution and percentile rank patterns is pivotal in shaping assessment strategies and grading policies. A balanced assessment design involves controlling for distribution skewness, ensuring sufficient score variability, and employing adaptive techniques that align Mu and percentile data to reinforce fairness.
Key strategies include:
- Implementing calibrated scoring scales that consider cohort-specific distribution features.
- Using percentile ranks in reporting to contextualize raw scores within the cohort’s performance landscape.
- Adjusting test difficulty levels to prevent clustering at score extremes, thereby maintaining a meaningful spread and preserving the interpretive value of Mu and percentile metrics.
Such measures foster equitable evaluation and transparent communication of student standing, especially critical when high-stakes decisions hinge on assessment outcomes.
Historical Context and Evolution of Grading Metrics

The interplay of Mu and percentile ranking transitions through historical shifts in educational measurement. In early educational models, absolute scores dominated, with little emphasis on cohort-based comparison. As psychometric theories matured, the adoption of standardized scoring and percentile ranks emerged to facilitate comparability across diverse populations and timeframes.
Advances in statistical modeling, including item response theory (IRT), further refined the relationship between raw scores, ability estimates, and performance percentiles. These innovations underscore the importance of integrating both distributional properties and relative rankings for comprehensive assessment systems.
Key Points
- The mean (Mu) provides a central measure but can be misleading if distributions are skewed or multi-modal.
- Percentile ranks offer relative standing, essential for performance comparisons, especially in diverse or non-normal cohorts.
- Understanding their relationship enhances assessment fairness and enables data-driven decision-making.
- Distribution shape, cohort heterogeneity, and test design collectively influence the alignment between Mu and percentile patterns.
- Adopting statistical awareness in grading strategies ensures equitable student evaluation and transparent reporting.
Conclusion: Synthesis and Future Directions
The nuanced relationship between Mu grade distribution and percentile rank patterns embodies the quintessence of modern educational measurement—balancing statistical rigor with pedagogical fairness. By dissecting their interdependence, educators and analysts can better interpret assessment data, refine grading practices, and ultimately foster a learning environment that genuinely reflects student achievement. Moving forward, integrating adaptive testing technologies, real-time distributional analytics, and multidimensional performance metrics promises to deepen this understanding and enhance the educational landscape’s evaluative precision.
How does skewness affect the relationship between Mu and percentile ranks?
+Skewness alters the symmetry of the score distribution, causing the mean (Mu) to deviate from the median. Positive skewness elevates Mu while many students still cluster at lower scores, impairing the interpretative power of Mu for percentile ranking. Accurate assessment requires recognizing these shifts and using additional metrics like median or percentile data for fair evaluation.
Why is it important to consider the shape of the score distribution in assessment design?
+The distribution shape influences how well the mean and percentile ranks correspond. For instance, skewed or multimodal distributions distort the typical relationship, potentially leading to misinterpretation of student performance if relying solely on Mu. Designing assessments that produce balanced, approximately normal distributions helps ensure fair and meaningful performance metrics.
What strategies can educators use to align Mu distribution with percentile patterns?
+Strategies include calibrating test difficulty to avoid excessive clustering at score extremes, employing adaptive testing to tailor difficulty levels, and reporting both raw scores along with percentile ranks. Regular analysis of score distributions and adjusting assessments accordingly help maintain alignment and fairness across cohorts.