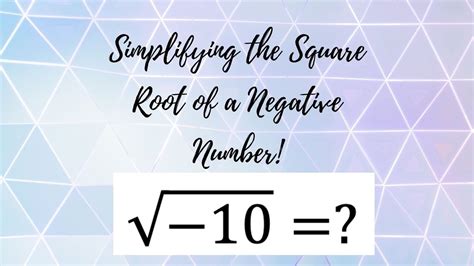The concept of square rooting a negative number has been a topic of interest and debate among mathematicians and scientists for centuries. At its core, the square root operation is defined as finding a value that, when multiplied by itself, gives a specified number. For instance, the square root of 16 is 4 because 4 multiplied by 4 equals 16. However, when we attempt to apply this operation to negative numbers, we encounter a significant challenge. In traditional real number mathematics, it is not possible to square root a negative number and obtain a real result, because no real number can be multiplied by itself to give a negative value.
Key Points
- The square root of a negative number cannot be expressed as a real number.
- Imaginary numbers, introduced by mathematicians, provide a way to extend the real number system to include square roots of negative numbers.
- The concept of imaginary numbers is fundamental in various branches of mathematics and science, including algebra, calculus, and physics.
- Imaginary numbers can be used to solve equations that cannot be solved using only real numbers.
- The use of imaginary numbers has numerous practical applications, such as in electrical engineering and signal processing.
Introduction to Imaginary Numbers

To address the limitation of real numbers, mathematicians introduced the concept of imaginary numbers. An imaginary number is defined as the square root of a negative number. For example, the square root of -1 is denoted by the symbol “i” (where i = √(-1)). This allows us to extend the real number system to the complex number system, which includes both real and imaginary components. A complex number can be represented in the form a + bi, where “a” is the real part, “b” is the imaginary part, and “i” is the imaginary unit.
Mathematical Representation and Operations
In mathematics, the square root of a negative number is represented using the imaginary unit “i”. For instance, √(-4) can be expressed as 2i, because (2i) * (2i) = 4 * i^2 = 4 * (-1) = -4. This representation enables us to perform various mathematical operations, such as addition, subtraction, multiplication, and division, on complex numbers. The rules for these operations are well-defined and allow us to manipulate complex numbers in a consistent and meaningful way.
| Mathematical Operation | Example |
|---|---|
| Addition | (2 + 3i) + (1 + 2i) = 3 + 5i |
| Subtraction | (2 + 3i) - (1 + 2i) = 1 + i |
| Multiplication | (2 + 3i) * (1 + 2i) = 2 + 4i + 3i + 6i^2 = 2 + 7i - 6 = -4 + 7i |
| Division | (2 + 3i) / (1 + 2i) = (2 + 3i) * (1 - 2i) / ((1 + 2i) * (1 - 2i)) = (2 - 4i + 3i - 6i^2) / (1 + 4) = (2 - i + 6) / 5 = 8/5 - i/5 |

Practical Applications of Imaginary Numbers

Imaginary numbers and complex numbers have numerous practical applications across various fields. In electrical engineering, complex numbers are used to represent AC circuits, where the impedance of a circuit can be represented as a complex number, including both resistance and reactance. In signal processing, complex numbers are used in the analysis and filtering of signals. The use of imaginary numbers also plays a crucial role in physics, particularly in the study of wave phenomena and quantum mechanics. The Schrödinger equation, which is central to quantum mechanics, relies heavily on complex numbers to describe the wave function of a quantum system.
Conclusion and Future Directions
In conclusion, while it is not possible to square root a negative number within the real number system, the introduction of imaginary numbers provides a powerful tool for extending our mathematical capabilities. The concept of imaginary numbers has far-reaching implications and applications in mathematics, science, and engineering. As we continue to explore and develop new mathematical frameworks and scientific theories, the importance of imaginary numbers and complex analysis is likely to grow, enabling us to tackle increasingly complex problems and deepen our understanding of the world around us.
What are imaginary numbers, and how are they used in mathematics?
+Imaginary numbers are an extension of the real number system, introduced to provide a solution to the square root of negative numbers. They are used in various mathematical operations and have applications in algebra, calculus, and other areas of mathematics and science.
Can imaginary numbers be used to solve real-world problems?
+Yes, imaginary numbers have numerous practical applications in fields such as electrical engineering, signal processing, and physics. They are used to represent AC circuits, analyze signals, and describe wave phenomena and quantum systems.
How do imaginary numbers relate to complex numbers?
+Imaginary numbers are a part of the complex number system, which includes both real and imaginary components. A complex number can be represented in the form a + bi, where “a” is the real part and “b” is the imaginary part.